O‘yinlar nazariyasining predmeti va asosiy tushunchalar

Muallif: Mengliyev SH.

Qo`shilgan sana: 2014-06-17

O‘yinlar nazariyasining predmeti va asosiy tushunchalar.
Ikki shaxsning nol yig’indili matritsaviy o‘yini.
Minimaks va maksimin strategiyalar.

Amaliyotda ko‘pincha boshqarish qarorlarini noaniqlik sharoitida qabul qilishga to‘g’ri keladi. Bunda noaniqlik qabul qilingan qarorning natijasiga ta’sir qiluvchi raqibning ongli xatti-xarakati tufayli xam yoki boshqa faktorlar tufayli xam bo‘lishi mumkin. Bir tomon qabul qilayotgan qarorlarning samaradorligi boshqa tomonning xatti-xarakatlariga bog’lik bo‘lgan vaziyatlar konfliktli (nizoli, ixtilofli) vaziyatlar deb ataladi. Konflikt tomonlar o‘rtasida albatta antogonistik ziddiyat bo‘lishini taqozo qilmaydi, lekin xamisha ma’lum bir tarzda tafovut bilan bog’lik bo‘ladi.
Konfliktli vaziyatlarni matematik tomondan analiz qiluvchi, uning matematik modelini tuzuvchi va tomonlarning ratsional xarakat qilish yo‘llarini o‘rganuvchi fan so-xasiga o‘yinlar nazariyasi deyiladi. O‘yinlar nazariyasining paydo bo‘lishi Dj.fon Neyman va O.Morgenshternlarning “O‘yinlar nazariyasi va iqtisodiy muomala” nomli monografiyasi bosilib chiqqan 1944 yil xisoblanadi.
Xozirgi vaqtda o‘yinlar nazariyasi gurkirab rivojlanmoqda. Uning antogonistik, noantogonistik (koopervtiv), chekli, cheksiz, pozitsion, differensial o‘yinlar va boshqa bir qator yo‘nalishlari mavjud. Keyingi paytlarda muxim axamiyat kasb etayotgan differensial o‘yinlar bir boshqariladigan ob’ektning boshqa boshqariladigan ob’ektni ta’kib qilishini ular xarakatlari dinamikasini xisobga olgan xolda o‘rganadi. Bunda ob’ektlar xarakati differensial tenglamalar yordamida tavsiflanadi.
O‘yin real konfliktli vaziyatning matematik modeli bo‘lib, u ma’lum qoidalar bo‘yicha taxlil qilinadi. Umumiy xolda o‘yin qoidalari yurishlar ketma-ketligini, xar bir tomonning qarshi tomon xarakatlari xaqidagi ma’lumoti xajmini va o‘yin natijasini (echimini) belgilaydi. Qoida, shuningdek, tanlashlarning mumkin bo‘lgan ma’lum ketma-ketligi amalga oshirilib, ortiq yurishlar qilish mumkin bo‘lmay qolgan o‘yining tugashini xam belgilaydi.
Ishtirokchilarning soniga qarab o‘yinlar juft va ko‘p tomonli bo‘ladilar. Juft o‘yinda ishtirokchilar soni ikkiga teng, ko‘p tomonli o‘yinda esa ularning soni ikkidan ortiq. Ko‘p tomonli o‘yin ishtirokchilari koalitsiyalar (ittifoqlar) tashkil qilishlari mumkin (bu xolda o‘yin koalitsion deb ataladi). Agar ko‘p tomonli o‘yin ishtirokchilari doimiy kaolitsiyaga birlashsalar u juft o‘yinga aylanadi.
O‘yinda (konfliktda) ishtirok etuvchi tomonlar o‘yinchilar deb ataladilar. Sport o‘yinida o‘yinchilar - bu aloxida sportchilar yoki komandalar bo‘lishi mumkin; xarbiy konfliktda - urushuvchi tomonlar; xalq xo‘jaligida - korxonalar, firmalar. Ba’zan o‘yinchi rolini tabiat xam bajaradi, chunki u qabul qilinishi kerak bo‘lgan qarorning shart-sharoitini shakllantiradi.
O‘yinchining strategiyasi deb uning xar bir shaxsiy yurishda o‘yin jarayonida yuz bergan vaziyatdan kelib chiqib tadbir variantini tanlash yo‘lini belgilovchi qoidalar majmuiga aytiladi.
Agar o‘yinchilarning strategiyalari soni chekli bo‘lsa, o‘yin chekli, agar o‘yinchilardan xech bo‘lmaganda bittasining strategiyalar soni cheksiz bo‘lsa - cheksiz deyiladi.
O‘yinchining strategiyasi unga maksimal yutuq yoki minimal qiymatli yutqazish bersa, bunday strategiya optimal strategiya deyiladi.
O‘yin qoidasida ko‘zda tutilgan strategiyalardan birini tanlash va uni amalga oshirish yurish deb ataladi.
Yurishlar shaxsiy va tasodifiy bo‘ladi. Agar o‘yinchi o‘zining tadbirlarining mumkin bo‘lgan variantlaridan birini ongli ravishda tanlasa (masalan, shaxmat va shashka o‘yinlaridagi xar qanday yurish), bunday yurishga shaxsiy yurish deyiladi. Agar tanlashni o‘yinchi emas, balkim biror tasodifiy tanlash mexanizmi (masalan, o‘yin soqqasini yoki tangani tashlash) bajarsa o‘yin tasodifiy deyiladi.
O‘yinlarni ta’riflashning ikki usuli mavjud: pozitsion va normal. Pozitsion usul o‘yinning yopik shakli bilan boglik bo‘lib, koidalar ketma-ketligining grafiga (o‘yin daraxtiga) keltiriladi. Normal usul o‘yinchilar strategiyalari to‘plami va to‘lov funk-siyasini oshkora ko‘rsatishdan iborat. O‘yinda to‘lov funksiyasi o‘yinchilar tanlagan strategiyaning xar bir to‘plami va to‘lov funksiyasini oshkora ko‘rsatishdan iborat. O‘yinda to‘lov funksiyasi o‘yinchilar tanlagan strategiyaning xar bir to‘plami uchun xar bir tomonning yutugini aniklaydi.
Agar juft o‘yinda bir o‘yinchining yutug’i ikkinchisining yutqizishiga teng bo‘lsa, bunday o‘yin nol yig’indili o‘yin deb ataladi.
Agar nol yig’indili o‘yinda ikki o‘yinchi qatnashsa, o‘yin antogonistik o‘yin xisoblanadi.
O‘yinlar nazariyasida nol yig’indili 2 shaxsning chekli o‘yini atroflicha o‘rganilgan.
Ikkita A va V o‘yinchilar qatnashgan antogonistik o‘yinni qaraymiz. O‘yinchilar qarama-qarshi maqsadni ko‘zlaydi. Biri qandaydir yutuqqa ega bo‘lsa, ikkinchisi shu miqdorda yutqazadi. Demak A o‘yinchining yutug’i V o‘yinchi yutug’ining teskari ishora bilan olinganiga teng bo‘lgani uchun biz bu o‘yinda A o‘yinchining yutug’ini taxlil qilsak yetarli.
A o‘yinchi (biz uni I o‘yinchi deymiz) m-ta A₁ , A₂ , ..,A_m strategiyalariga, V o‘yinchi (biz uni II o‘yinchi deymiz) n-ta V₁ , V₂ ,.., V_n strategiyalarga ega bo‘lsin. Bunday o‘yinga mxn o‘lchamli o‘yin deyiladi.
I o‘yinchi o‘zining mumkin bo‘lgan strategiyalaridan biri A_i ni, i=1,2..,m, II o‘yinchi esa, I o‘yinchining tanlash natijasidan bexabar xolda, V_j strategiyani (j=1,2..,n) tanlangan bo‘lsin. Strategiyalarni tanlash natijasida I o‘yinchining yutug’i W₁(A_i ,B_j) va II o‘yinchining yutug’i W₂(A_i ,B_j) bo‘lsa, ular W₁₍A_i ,B_j) +
+W₂(A_i ,B_j)=0 munosabatni qanoatlantiradi. Agar W(A_i ,B_j)= W₁(A_i ,B_j) deb olsak, W₂(A_i ,B_j)= -W(A_i ,B_j bo‘ladi.
W(Ai,Bj)=aij deb belgilaylik. Faraz qilaylikki, aij ning qiymatlari strategiyalarning xar bir jufti uchun bizga ma’lum bo‘lsin. Bu qiymatlarni satrlari I o‘yinchining strategiyalariga, ustunlari esa II o‘yinchining strategiyalariga mos keladigan jadval (1-jadval) ko‘rinishida yozamiz. Bunday jadval to‘lov matritsasi deb ataladi.

1-jadval

II I	B₁	B₂	. . .	B_n
A₁	a₁₁	a₁₂	...	A_1n
A₂	a₂₁	a₂₂	...	A_2n
...	...	...	...
A_m	a_m1	a_m2	...	A_mn

Matritsaning xar bir musbat aij elementi mos strategiyalar qo‘llanilganda I o‘yinchining yutug’i va II o‘yinchining yutqizishi miqdorini bildiradi. I o‘yinchining maqsadi - o‘z yutug’ini maksimallashtirish, II o‘yinchining maqsadi esa - o‘z yutqizishini minimallashtirishdir.
1-misol. O‘yinda I va II o‘yinchilar ishtirok qiladilar. O‘yinchilardan xar biri boshqasidan bexabar xolda 1, 2 yoki 3 ta barmog’ini ko‘rsatishi mumkin. Agar I va II o‘yinchilar ko‘rsatgan barmoqlar soni o‘rtasidagi ayirma musbat bo‘lsa, I o‘yinchi shu sonlar ayirmasi qadar ochko yutadi va aksincha, agar ayirma manfiy bo‘lsa, II o‘yinchi shuncha yutadi. Agar sonlar o‘rtasidagi ayirma nol bo‘lsa, o‘yin durang bilan tugaydi.
O‘yinda xar bir o‘yinchining uchtadan shaxsiy yurishi bor. I o‘yinchida uchta strategiya bor: A₁ - 1 ta barmoqni ko‘rsatish, A₂ - 2 ta barmoqni ko‘rsatish, A₃ – 3 ta barmoqni ko‘rsatish. II o‘yinchida (rakibda) xam uchta strategiya bor: V₁ – 1 ta, V₂ – 2 ta, V₃ – 3 ta barmoqni ko‘rsatishdan iborat. O‘yinchilarning ular tegishli strategiyalarni qo’llaganlardagi yutuqlarini to‘lov matritsasi (2-jadval) ko‘rinishida yozib qo‘yamiz.

2-jadval

II I	B₁=1	B₂=2	B₃=3
A₁=1	0	-1	-2
A₂=2	1	0	-1
A₃=3	2	1	0

Bu matritsa elementlari qanday xosil qilinganligini ko‘ramiz. Agar I o‘yinchi A₁ strategiyani II o‘yinchi V₃ strategiyani qo‘llasa, u vaqtda I o‘yinchi ikki birlik yutqazadi. To‘lov matritsasida bu yutqazish birinchi satr va uchinchi ustunlar kesishishidagi (1;3) katakka yozilgan. Agar I o‘yinchi A₂ strategiyasi, raqib esa V₁ strategiyani qo‘llasa, u xolda I o‘yinchi bir birlik yutadi. To‘lov matritsasida bu yutuq (2;1) katakka musbat ishora bilan yozib qo‘yilgan. Jadvalning boshqa elementlari xam shu tariqa xosil qilingan.
Tulov matritsasi 3-jadvalda keltirilgan mxn-o‘yinni karaymiz. Masala A₁, A₂,...,A_m strategiyalar orasidan I o‘yinchining eng yaxshi strategiyasini va B₁, B₂, ...,B_n strategiyalar ichidan II o’yinchining eng yaxshi strategiyasini topishdan iborat. Bu masalani yechishda uyinda ishtirok etuvchi rakiblar bir xil akl-idorkka ega va ulardan xar biri uz maksadiga erishish uchun xamma chora-tadbirlarni ko’radi deb xisoblaymiz. Bu tamoyildan foydalanib I o’yinchining eng yaxshi strategiyasini topamiz. Buning uchun uning xamma strategiyalarini ketma-ket taxlil qilamiz. I o‘yinchi o‘zining A_i strategiyasini tanlaganda biz unga II o‘yinchi o‘zining I o‘yinchi yutug’ini minimallashtiruvchi V_j strategiyasi bilan javob beradi deb xisoblashimiz kerak. Shunga ko‘ra to‘lov matritsasining xar bir satridagi a_ij sonlar ichida minimal sonni topamiz va uni bilan belgilab, to‘lov matritsasining yonidan qo‘shimcha ustunga yozib qo‘yamiz:

. (1)
sonlarni bilgan A o‘yinchi o‘zining strategiyalari ichida shundayini tanlaydiki, u eng katta yutuq bersin. Bu maksimal yutuqni deb belgilaymiz, ya’ni . Shunday qilib, (1) ni xisobga olsak, 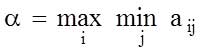xosil bo‘ladi.
soni I o‘yinchining kafolatli yutug’i bo‘lib, o‘yinning quyi baxosi (maksimini) deb ataladi. O‘yinning quyi baxosi ni yutishni ta’minlovchi strategiya maksimin strategiya deb ataladi. Agar I o‘yinchi o‘zining maksimin strategiyasiga amal qilsa, II o‘yinchi qanday yo‘l tutishidan qa’tiy nazar, unga dan kam bo‘lmagan yutuq ta’minlanadi.

3-jadval

II I	B₁	B₂	...	B_n
A₁	a₁₁	a₁₂	...	a_1n
A₂	a₂₁	a₂₂	...	a_2n
...	...	...	...	...
A_m	a_m1	a_m2	...	A_mn

II o‘yinchi o‘z yutqizishini kamaytirishga, ya’ni I o‘yinchi yutug’ini minimumga aylantirishga xarakat qiladi. Shu sababli o‘zining eng yaxshi strategiyasini tanlab olish uchun u to‘lov matritsasi ustunlarining xar biridagi maksimal sonni topish va bu qiymatlar orasidan eng kichigini tanlab olishi kerak.
Xar bir ustundagi maksimal elementni deb belgilaymiz va bu elementlarni 4-jadvalning qo‘shimcha satriga yozib qo‘yamiz. lar orasidan eng kichik qiymatlisini deb belgilaymiz. - o‘yinning yuqori baxosi (minimaksi) bo‘lib, u formula bo‘yicha topiladi.
II o‘yinchiga “yutuqni” ta’minlaydigan strategiya uning minimaks strategiyasi deb ataladi. Agar II o‘yinchi o‘zining minimaks strategiyasiga amal qilsa, xar qanday xolda xam uning yutqizishi dan oshmaydi.

4-jadval

II I	B₁	B₂	...	B_n	a_i
A₁	a₁₁	a₁₂	...	a_1n	a₁
A₂	a₂₁	a₂₂	...	a_2n	a₂
...	...	...	...	...	...
A_m	a_m1	a_m2	...	a_mn	a_m
b_j	b₁	b₂	...	b_n

O‘yinning quyi va yuqori baxolari uchun tengsizlikning xamisha o‘rinli, ya’ni ekanligini ko‘rsatish mumkin.
Xaqiqatan xam, faraz qilaylikki va bo‘lsin. U vaqtda, va larning aniqlanishiga ko‘ra, .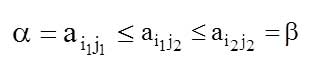
Quyi va yuqori baxolari o‘zaro teng, ya’ni bo‘lgan o‘yinlar mavjud. Bunday o‘yinlar egar nuqtali o‘yinlar deb ataladi.
Egar nuqtali o‘yinlarda yuqori va quyi baxolarining umumiy qiymati o‘yining sof baxosi, bu qiymatga erishishni ta’minlovchi va strategiyalar esa optimal strategiyalar deyiladi.
Optimal strategiyalarning jufti tulov matritsasining (o‘yinning) egar nuqtasi deb ataladi. element bir vaqtning o‘zida i - satrda minimal, j - ustunda maksimaldir.
Optimal strategiyalar va sof qiymat o‘yinning yechimi xisoblanadi.
Optimal strategiyalar muxim xususiyatga egadir. Ular o‘yinda shunday “muvozanat xo-latini” bildiradiki, xar bir o‘yinchi o‘zining optimal strategiyasidan chetga chiqishdan manfaatdor emas, chunki bundan u foyda qilmaydi. Egar nuqtali o‘yinda raqiblar bir xil aql-idrokli deb xisoblansa, o‘yinning sof baxosi ni I o‘yinchi oshira olmaydi, II o‘yinchi esa kamaytira olmaydi.
Agar o‘yin egar nuqtaga ega bo‘lsa, u sof strategiyalarda yechiladi deyiladi.
Sof strategiyalar deganda o‘yinchi tomonidan, tasodifiy tanlash mexanizmini ishlatmasdan, ongli ravishda tanlangan strategiya tushuniladi.
To‘lov matritsasi bir necha egar nuqtalarga ega bo‘lishi mumkin.
2-misol. To‘lov matritsasi 2- jadvalda keltirilgan U o‘yinning yechimi topilsin.
va larning qiymatlarini topib, ularni 5- jadvalga yozib qo‘yamiz.

5- jadval

II I	B₁ =1	B₂=2	B₃=3
A₁=1	0	-1	-2	-2
A₂=2	1	0	-1	-1
A₃=3	2	1	0	0
	2	1	0

O‘yinning quyi baxosi
.
O‘yinning yuqori baxosi
.
bo‘lgani uchun o‘yin egar nuqtaga ega. O‘yinning sof baxosi . Optimal strategiyalar: I o‘yinning A₃ strategiyasi va II o‘yinchining V₃ strategiyasi. Egar nusta esa (A₃ ,V₃) bo‘ladi.
3- misol. To‘lov matritsasi 6- jadvalda keltirilgan U o‘yinnining yechimi topilsin.
va larning qiymatlarini topamiz va ularni 6- jadvalga kiritamiz.

6- jadval

II I	B₁	B₂	B₃	B₄
A₁	6	5	8	5	5
A₂	7	3	2	3	2
A₃	6	5	7	5	5
	7	5	8	5

O‘yinning quyi va yuqori baxolarini topamiz:

.
va ning qiymatlaridan ko‘rinib turibdiki, o‘yin matritsasi optimal strategiyalarning A₁V₂, A₁V₄, A₃V₂, A₃V₄ juftlariga mos to‘rtta egar nuqtaga ega. O‘yinning sof baxosi =5.

21529 marta o`qildi.

shoydullo adminstrator

I

I

I

I